Integral de Borwein

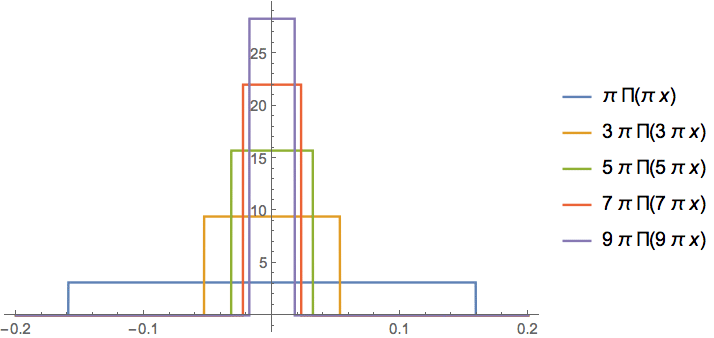
En matemáticas, una integral de Borwein es una integral con unas propiedades peculiares presentada por primera vez por los matemáticos David Borwein y Jonathan Borwein en 2001.^[1]​ Las integrales de Borwein utilizan productos de senos cardinales sinc(ax), donde la función seno cardinal se define como sinc(x) = sen(x)/x para x distinto de 0, y sinc(0) = 1.^[1]​^[2]​

Estas integrales presentan un aparente patrón regular que acaba rompiéndose de repente. Así,

${\displaystyle {\begin{aligned}&\int _{0}^{\infty }{\frac {\operatorname {sen}(x)}{x}}\,dx={\frac {\pi }{2}}\\[10pt]&\int _{0}^{\infty }{\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}\,dx={\frac {\pi }{2}}\\[10pt]&\int _{0}^{\infty }{\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}{\frac {\operatorname {sen}(x/5)}{x/5}}\,dx={\frac {\pi }{2}}\end{aligned}}}$

Este esquema continúa hasta

${\displaystyle \int _{0}^{\infty }{\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}\cdots {\frac {\operatorname {sen}(x/13)}{x/13}}\,dx={\frac {\pi }{2}}.}$

Sin embargo, con el siguiente término, se produce el siguiente resultado:

${\displaystyle {\begin{aligned}\int _{0}^{\infty }{\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}\cdots {\frac {\operatorname {sen}(x/15)}{x/15}}\,dx&={\frac {467807924713440738696537864469}{935615849440640907310521750000}}~\pi \\[5pt]&={\frac {\pi }{2}}-{\frac {6879714958723010531}{935615849440640907310521750000}}~\pi \\[5pt]&\approx {\frac {\pi }{2}}-2.31\times 10^{-11}.\end{aligned}}}$

En general, estas integrales tienen por valor π/2 cuando los denominadores impares 3, 5, 7… son sustituidos por cualesquier números reales positivos tales que la suma de sus inversos es menor que 1.

En el ejemplo anterior, 1/3 1/5 … 1/13 < 1, pero 1/3 1/5 … 1/15 > 1.

Al incluir el factor adicional ${\displaystyle 2\cos(x)}$ en las integrales, el mismo patrón se mantiene durante más tiempo, concretamente se mantiene para los impares desde el 1 hasta en 111:

${\displaystyle \int _{0}^{\infty }2\cos(x){\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}\cdots {\frac {\operatorname {sen}(x/111)}{x/111}}\,dx={\frac {\pi }{2}},}$

sin embargo para el siguiente,

${\displaystyle \int _{0}^{\infty }2\cos(x){\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}\cdots {\frac {\operatorname {sen}(x/111)}{x/111}}{\frac {\operatorname {sen}(x/113)}{x/113}}\,dx\approx {\frac {\pi }{2}}-2.3324\times 10^{-138}.}$

En este caso el patrón se rompe porque 1/3 1/5 … 1/111 < 2, pero 1/3 1/5 … 1/113 > 2. El valor exacto de esta integral puede ser calculado mediante una fórmula general. Desarrollado, este valor concreto es:

${\displaystyle {\frac {\pi }{2}}\left(1-{\frac {3\cdot 5\cdots 113\cdot ({\frac {1}{3}} {\frac {1}{5}} \cdots {\frac {1}{113}}-2)^{56}}{2^{55}\cdot 56!}}\right),}$

lo cual es una fracción que involucra dos números de 2736 cifras.

El motivo por el que estos patrones, tanto el original como el extendido mediante el coseno, se acaban rompiendo se ha podido probar mediante una demostración intuitiva.^[3]​

Fórmula general

Dada una sucesión de números reales distintos de 0, ${\displaystyle a_{0},a_{1},a_{2},\ldots }$, se puede construir una fórmula general para la integral^[1]​

${\displaystyle \int _{0}^{\infty }\prod _{k=0}^{n}{\frac {\operatorname {sen}(a_{k}x)}{a_{k}x}}\,dx}$

Para establecer la fórmula, habrá que considerar las sumas a partir de los ${\displaystyle a_{k}}$. En particular, si ${\displaystyle \gamma =(\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})\in \{\pm 1\}^{n}}$ es una ${\displaystyle n}$-upla donde cada uno de los términos es ${\displaystyle \pm 1}$, entonces se puede escribir ${\displaystyle b_{\gamma }=a_{0} \gamma _{1}a_{1} \gamma _{2}a_{2} \cdots \gamma _{n}a_{n}}$, que es una especie de suma alterna de los ${\displaystyle a_{k}}$, y se puede establecer ${\displaystyle \varepsilon _{\gamma }=\gamma _{1}\gamma _{2}\cdots \gamma _{n}}$, que puede ser 1 o -1. Con esta notación, el valor de esta integral es

${\displaystyle \int _{0}^{\infty }\prod _{k=0}^{n}{\frac {\operatorname {sen}(a_{k}x)}{a_{k}x}}\,dx={\frac {\pi }{2a_{0}}}C_{n}}$

donde

${\displaystyle C_{n}={\frac {1}{2^{n}n!\prod _{k=1}^{n}a_{k}}}\sum _{\gamma \in \{\pm 1\}^{n}}\varepsilon _{\gamma }b_{\gamma }^{n}\operatorname {sgn}(b_{\gamma })}$

En el caso en que ${\displaystyle a_{0}>|a_{1}| |a_{2}| \cdots |a_{n}|}$, se tiene ${\displaystyle C_{n}=1}$.

Además, si hay un ${\displaystyle n}$ tal que para cada ${\displaystyle k=0,\ldots ,n-1}$ tenemos ${\displaystyle 0$ y ${\displaystyle a_{1} a_{2} \cdots a_{n-1}$, que significa que ${\displaystyle n}$ es el primer valor cuando la suma parcial de los ${\displaystyle n}$ primeros elementos de la sucesión excede de ${\displaystyle a_{0}}$, entonces ${\displaystyle C_{k}=1}$ para cada ${\displaystyle k=0,\ldots ,n-1}$, pero

${\displaystyle C_{n}=1-{\frac {(a_{1} a_{2} \cdots a_{n}-a_{0})^{n}}{2^{n-1}n!\prod _{k=1}^{n}a_{k}}}}$

El primer ejemplo es el caso cuando ${\displaystyle a_{k}={\frac {1}{2k 1}}}$.

Nótese que, si ${\displaystyle n=7}$, entonces ${\displaystyle a_{7}={\frac {1}{15}}}$ and ${\displaystyle {\frac {1}{3}} {\frac {1}{5}} {\frac {1}{7}} {\frac {1}{9}} {\frac {1}{11}} {\frac {1}{13}}\approx 0.955}$, pero ${\displaystyle {\frac {1}{3}} {\frac {1}{5}} {\frac {1}{7}} {\frac {1}{9}} {\frac {1}{11}} {\frac {1}{13}} {\frac {1}{15}}\approx 1.02}$, por lo que, como ${\displaystyle a_{0}=1}$, tenemos que

${\displaystyle \int _{0}^{\infty }{\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}\cdots {\frac {\operatorname {sen}(x/13)}{x/13}}\,dx={\frac {\pi }{2}}}$

que se sigue cumpliendo incluso al eliminar cualquiera de los productos, pero

${\displaystyle {\begin{aligned}&\int _{0}^{\infty }{\frac {\operatorname {sen}(x)}{x}}{\frac {\operatorname {sen}(x/3)}{x/3}}\cdots {\frac {\operatorname {sen}(x/15)}{x/15}}\,dx\\[5pt]={}&{\frac {\pi }{2}}\left(1-{\frac {(3^{-1} 5^{-1} 7^{-1} 9^{-1} 11^{-1} 13^{-1} 15^{-1}-1)^{7}}{2^{6}\cdot 7!\cdot (1/3\cdot 1/5\cdot 1/7\cdot 1/9\cdot 1/11\cdot 1/13\cdot 1/15)}}\right)\end{aligned}}}$

que es igual al valor dado anteriormente.

Referencias

Enlaces externos

• «La curiosa y desconcertante integral de Borwein». Microsiervos. Consultado el 5 de diciembre de 2018. 
• «Patterns That Eventually Fail». Azimuth (en inglés). 20 de septiembre de 2018. Consultado el 5 de diciembre de 2018. 
• «Breakdown». Futility Closet (en inglés). 2 de febrero de 2018. Consultado el 5 de diciembre de 2018.